One of the basic principles of cryptography is that according to Kerckhoff’s hypothesis [VAC1], it is assumed that the overall security of any cryptosystem is completely dependent on the security of the key, and that all other parameters of the crypto system are publicly observable. Thus, the cryptographic algorithms are assumed as open as long as the key generation scheme is not secure. In real life, many systems actually use well-known symmetric and asymmetric cryptographic algorithms (AES, 3DES, RSA, ECDSA, SHA) which have been applied in many domains and all experts are aware of their strengths and weaknesses.

Vulnerability analysis is complementary to cryptography. The robustness of a crypto system depends on the key used, or in other words, the attacker’s ability to predict the key. The hardware-based vulnerability analysis of key generation relies on 4 steps (Figure ‎3.12):

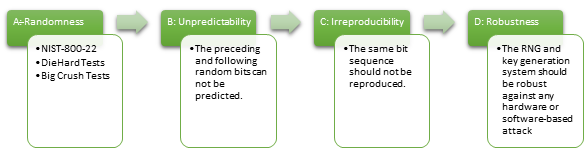
A: Randomness: There are two basic types of generators used to produce random sequences: true random number generators (TRNGs) and pseudorandom number generators (PRNGs) [VAC2]. TRNGs generate random numbers from a physical process (thermal noise, the photoelectric effect, ring oscillator) rather than by means of an algorithm. While TRNGs take the advantage of non-deterministic entropy sources, PRNGs generate bits in a deterministic manner. The PRNG-generated sequence is not truly random, because it is completely determined by an initial value, called the PRNG's seed (which may include truly random values). PRNGs tend to benefit from the external source of randomness (e.g., mouse movements, delay between keyboard presses etc.) which are practical in use but predictable either. In other words, an attacker can easily guess the outputs of a PRNG by applying statistical or machine learning methods so that the cryptographic keys or secrets (which uses the bit streams as outputs of PRNGs) also become guessable (the previous or next bits can be predicted). The first thing to apply for the vulnerability analysis of a cryptosystem is to check whether the system relies on a hardware-based RNG or not. Then, this RNG should be TRNG. To meet the true randomness criteria, three test suites are applied on a sufficient length of bit sequences: I) NIST-800-22 Randomness Test Suite [VAC3]; II) DieHard Test Suite [VAC4]; III) Big Crush Test Suite [VAC5]

The typical outputs of a TRNG must pass all 15 criteria of NIST-800-22 Randomness Test Suite which are listed as:  i) Frequency (Monobit) ; ii) Frequency Test within a Block; iii) Runs; iv) Longest-Run-of-Ones in a Block; v) Binary Matrix Rank; vi) Discrete Fourier Transform (Spectral); vii) Non-overlapping Template Matching; viii) Overlapping Template Matching; ix) Maurer's "Universal Statistical"; x) Linear Complexity; xi) Serial ; xii) Approximate Entropy; xiii) Cumulative Sums (Cusums); xiv) Random Excursions; xv) Random Excursions Variant. Diehard and Big Crush Test Suites also cover additional criteria that should be met to evaluate the randomness.

B. Unpredictability:  The randomness test suites [VAC3-5] are useful but the main message given by these tests is that the tested sequence is NOT random. As they rely on statistical techniques the randomness test suites do not give any guarantee about the true randomness of a bit sequence. Even if a bit sequence fulfils all the randomness test suites, they cannot present any quantification about their predictability. In order to say that a TRNG is reliable, the preceding and following random bits generated by the TRNG cannot be predicted by any technique. Although there exist alternative methods, the proposed predictability analysis was presented in [VAC6].

An ideal entropy source which is used as the core of a TRNG based on thresholding random noise should have constant power spectral density over its operating bandwidth. The proposed vulnerability analysis technique in VALU3S relies on the generation of independent and uniformly distributed bits, per-sample joint entropy of the generated bit sequence and the autocorrelation function of the output (also addressed in [VAC6]). Here, it is assumed that the underlying noise waveform is a continuous-time wide sense stationary Gaussian process, of which power spectral density is flat between two known frequencies. Given a continuous time wide-sense stationary flat band-limited Gaussian noise source, the test aims to investigate the necessary and sufficient conditions for generating independent and identically distributed random bits with uniform marginal probabilities via uniformly sampling from this process and providing analytical and numerical results for the per-sample joint entropy. This is realised by preparing an equivalent setup in place of the original one in order to make the derivations simpler.

C: Irreproducibility & D: Robustness: The strength of a crypto system almost depends on the strength of the key used or in other words on the difficulty for an attacker not only to predict the key but also assure the irreproducibility of the same bit sequence and recommend a robust design against attacks. The TRNGs should not rely on the deterministic sources, otherwise one can even predict the secret parameters of RNGs [VAC7]. In recent years, the majority of the TRNGs rely on non-linear systems, e.g. chaotic RNGs. So, in C and D, the vulnerability analysis of the TRNG is tackled so that the irreproducibility and robustness against attacks is jointly encountered.

This is realised by a novel predicting system (as addressed in [VAC6-9]) that is proposed to find out the security weaknesses of a chaotic RNG. Convergence of the predicting system is proved using auto-synchronization. Secret parameter of the target chaotic RNG is revealed where the public information is the design of the chaotic RNG and a scalar time series observed from the target chaotic system. Simulation and numerical results verifying the feasibility of the predicting system are also given similar to the recent papers of ERARGE [VAC8, VAC7, VAC9] such that next bit can be predicted as well while the same output bit sequence of the chaotic RNG can be regenerated.