Runtime verification is a pragmatic, yet rigorous, technique to reason about software and systems in a systematic manner. It borrows the concept of formal specifications and combines it with the analysis of individual system behaviours. Thus, this technique does not encounter the scalability issues that are commonly associated to the formal verification. Runtime verification is a black-box method that does not require an abstract model. As a consequence, it can be used both at the design and the deployment time of a system. Runtime verification has found its way in many application areas, including the field of monitoring CPS.

Signal Temporal Logic (STL) [TOO1] is a specification formalism for expressing real-time temporal properties of CPS. In its original form, STL was designed as a declarative specification language for runtime monitoring. We can see STL specifications as binary classifiers that partition behaviours into good and bad ones (Figure ‎3.6). The following requirement is a typical example of an informal English specification that describes the rising of a continuous signal and can be naturally formalized in STL:

“The rise time of the voltage V from V_min to V_max must be smaller or equal than T_rise is”.

The STL specification that describes the above requirement is expressed as follows.

v_l = (V ≤ V_low);

v_m = (V > V_low and V ≤ V_high);

v_h = (V > V_high);

always (v_l → (v_m until[0,T_rise] v_h));

Figure ‎3.6 Good vs. Bad Behaviours

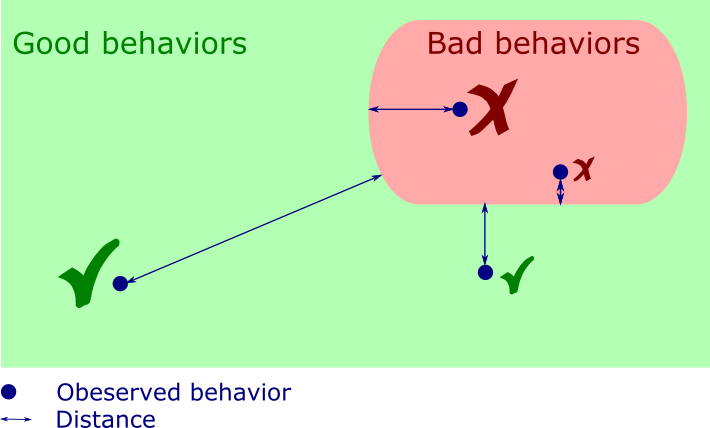
Quantitative semantics of specification languages: Consider the predicate x ≥ 5 and the valuation in which x equals to 2. The qualitative evaluation of this simple specification tells us that the valuation violates the property. Given this numerical predicate over a real-valued variable and a variable valuation, we can also answer the question on how far the valuation is from satisfying or violating the predicate. This rich feedback contrasts the classical yes/no answer that we typically get from reasoning about Boolean formulas. Fainekos and Papas [TOO2] lifted this quantitative property of numerical predicates to the temporal case, giving rise to the quantitative semantics for STL. This extension replaces the binary satisfaction relation with a real valued robustness degree function while preserving the syntax of the specification language. The robustness degree indicates how far an observed signal from satisfying or violating the specification is. The original quantitative STL semantics have been defined in terms of the infinite form. This spatial notion of robustness was consequently extended in several directions, including time robustness and average robustness. The quantitative semantics is a powerful extension that allows ordering specifications according to their goodness or badness and opens up the possibility of building new applications.

Applications: Runtime verification is a versatile technology that has been successfully combined with many other analysis and synthesis methods. In particular, STL qualitative and quantitative monitors have been used as the basis for many new techniques for analysing CPS, such as falsification-based testing [TOO3], parameter synthesis [TOO4], specification mining [TOO5], and fault explanation [TOO6, TOO7].